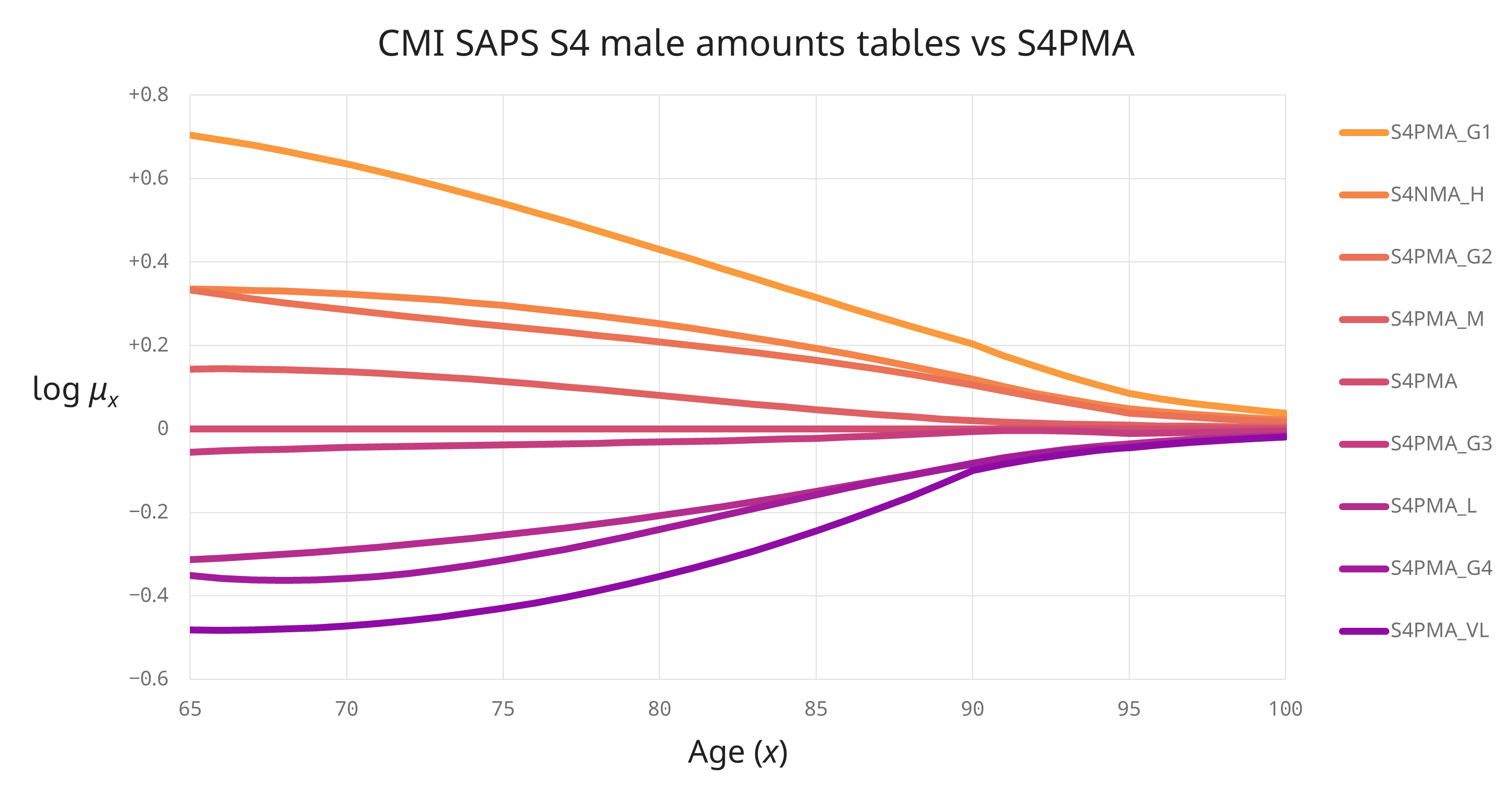
Mortality: Good things come to those who weight (III)
This is the final article of three on weighted mortality analysis.
If you haven’t already read Part I then I recommend you do that first.
And if you’re really keen to understand the maths then give Part II a go, but it’s not essential.
In this article, I’ll review the implications and provide some practical recommendations.